Расчет площади разностороннего треугольника онлайн с использованием формулы

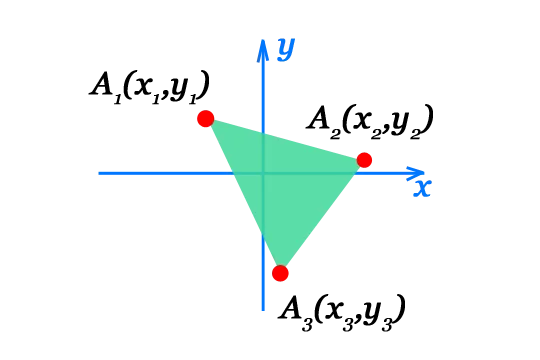
Вычислить площадь треугольника разностороннего

Используя онлайн калькулятор, вы можете легко определить площадь треугольника с разными сторонами с помощью соответствующих формул. Для того чтобы выполнить вычисление площади треугольника с разными сторонами, просто внесите необходимые данные.

1. Площадь треугольника разностороннего через две стороны и угол между ними.
2. Площадь треугольника разностороннего через радиус описанной окружности и три стороны.
3. Площадь треугольника разностороннего через диаметр описанной окружности и три стороны.
4. Площадь треугольника разностороннего через площадь описанного круга и три стороны.
5. Площадь треугольника разностороннего через длину описанной окружности(периметр) и три стороны.
6. Площадь треугольника разностороннего через радиус вписанной окружности и три стороны.
7. Площадь треугольника разностороннего через диаметр вписанной окружности и три стороны.
8. Площадь треугольника разностороннего через площадь вписанного круга и три стороны.
9. Площадь треугольника разностороннего через длину (периметр) вписанной окружности и три стороны.
10. Площадь треугольника разностороннего через сторону и два прилегающих угла.
11. Площадь треугольника разностороннего по формуле Герона.

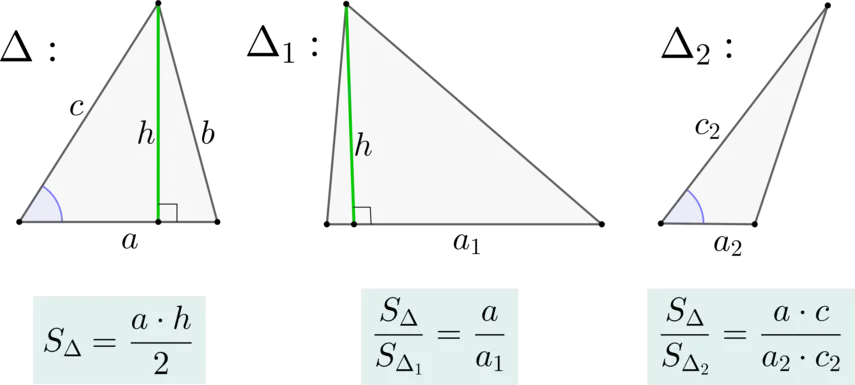
1. Площадь треугольника разностороннего равна половине произведения его основания на высоту.
2. Площадь треугольника разностороннего — это положительная величина той части плоскости, которую занимает разносторонний треугольник.

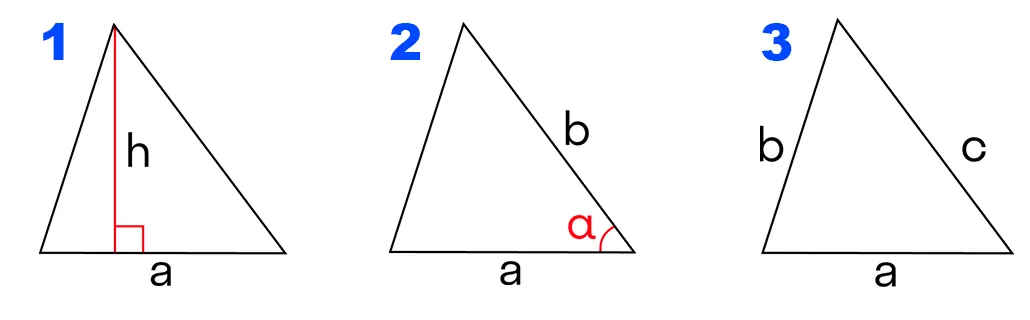
Площадь треугольника разностороннего через две стороны и угол между ними.

S = ab · sin(α)

Где: a, b — стороны треугольника разностороннего, α — угол между сторонами.

Площадь треугольника разностороннего через радиус описанной окружности и три стороны.

S = abc4R

Где: a, b, c — стороны треугольника разностороннего, R — радиус описанной окружности.

Площадь треугольника разностороннего через диаметр описанной окружности и три стороны.

S = abc2D

Где: a, b, c — стороны треугольника разностороннего, D — диаметр описанной окружности.

Площадь треугольника разностороннего через площадь описанного круга и три стороны.

Где: a, b, c — стороны треугольника разностороннего, S — площадь описанного круга.

Площадь треугольника разностороннего через длину описанной окружности(периметр) и три стороны.

S = abc2 Pπ

Где: a, b, c — стороны треугольника разностороннего, P — периметр описанной окружности, π — 3,14.

Площадь треугольника разностороннего через радиус вписанной окружности и три стороны.

S = R a + b + c

Где: a, b, c — стороны треугольника разностороннего, R — радиус вписанной окружности, π — 3,14.

Площадь треугольника разностороннего через диаметр вписанной окружности и три стороны.

S = D a + b + c

Где: a, b, c — стороны треугольника разностороннего, D — диаметр вписанной окружности, π — 3,14.

Площадь треугольника разностороннего через площадь вписанного круга и три стороны.

Видео. найти площадь треугольника. Формула Герона. Известны 3 стороны.

Где: a, b, c — стороны треугольника разностороннего, S — площадь вписанного круга.

Площадь треугольника разностороннего через длину (периметр) вписанной окружности и три стороны.

S = Pπ · a + b + c

Где: P — периметр вписанной окружности, a, b, c — стороны разностороннего треугольника.

Площадь треугольника разностороннего через сторону и два прилегающих угла.

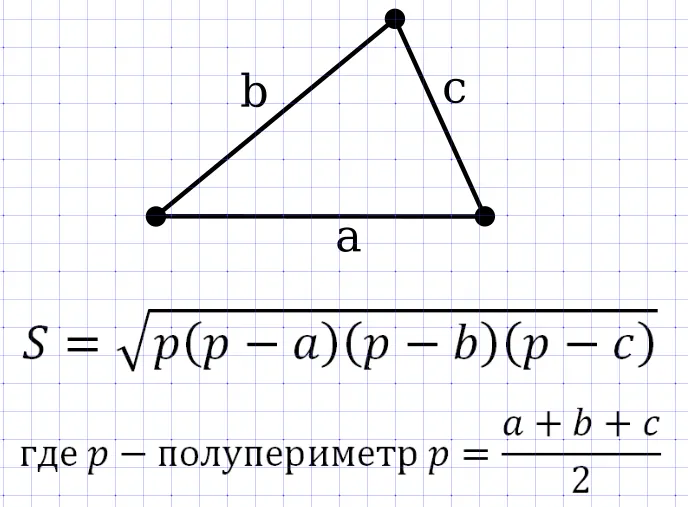
S = a 2 · sin(α) · sin(β) sin(180 — (α + β))

Где: α, β — прилегающие углы к стороне, a — сторона.

Площадь треугольника разностороннего по формуле Герона.

P = a + b + c

Где: a, b — катеты треугольника разностороннего, с — гипотенуза треугольника разностороннего, P — полупериметр прямоугольного треугольника.

Как вычислить окружность?

Окружность — это геометрическая фигура, которая состоит из всех точек на плоскости, находящихся на одном и том же расстоянии от фиксированной точки, называемой центром окружности.

Для вычисления окружности нужно знать ее радиус (расстояние от центра окружности до любой точки на окружности) или диаметр (расстояние между двумя точками на окружности через ее центр).

Для вычисления окружности по радиусу нужно умножить диаметр на число π (пи), которое равно примерно 3,14 или 22/7.

Формула для вычисления окружности: C = 2πr, где С — длина окружности, r — радиус окружности, π — число пи (примерно 3,14).

Для примера, если радиус окружности равен 5 см, то ее длина будет C = 2πr = 2 * 3,14 * 5 = 31,4 см. Таким образом, длина окружности равна 31,4 см.

Видео. Найдите площадь треугольника на рисунке ★ Два способа решения